Tanácsok matek felvételihez 8. osztályosoknak
A felvételi komoly mérföldkő egy diák életében, hiszen ezen is múlik, sikerül-e a választott iskolában folytatnia a tanulmányait. Mivel a matematika sokaknak mumusnak számít, így tapasztalatom szerint a diákok nagyon félnek ettől a felvételitől. De van egy jó hírem … a középiskolai matematika felvételi típus feladatokból (pontosabban típus témakörökből) áll, így remekül fel lehet készülni rá! Természetesen a feladatok az adott témakörön belül mindig mások, de – kis túlzással - ugyanúgy kell megoldani őket, így a megoldási módszereket a korábbi évek feladatain keresztül jól be lehet gyakorolni. Ebben szeretnék segíteni a középiskolába matematikából felvételiző 8. osztályos diákoknak oly módon, hogy feladattípusról feladattípusra haladva felelevenítem a legszükségesebb tudnivalókat és tippeket adok az adott feladattípus megoldásához.
1. feladat
Az első feladat túlnyomórészt a törtekről szól. Ezek legtöbbször közönséges törtek, de előfordulnak időnként tizedestörtek, vegyes törtek, sőt, vegyesen is. Alapvető műveleteket kell elvégezni, ezért ezekkel nagyon tisztában kell lenni, hogy ne menjen el sok idő a megoldással. Ezeket a feladatokat „csípőből” kell megoldani, gyakorlatilag gondolkodás nélkül. Nézzük, miket kell tudni róluk.
0. Közönséges törtekkel való számolás előtt mindig nézzük meg, lehet-e egyszerűsíteni!!! Az egyszerűsítés lehetőségét folyamatosan figyeljük, minden részszámítás után nézzük meg! (Többször volt már olyan feladat a felvételin, hogy ha valaki egyszerűsítés nélkül kezdte el a műveleteket elvégezni, nagy számokkal kellett dolgoznia, míg ha egyszerűsített volna, gyakorlatilag számolás nélkül megkapta volna a helyes eredményt.) Ne feledjük, hogy írásbeli osztás esetén is lehet egyszerűsíteni az osztandó és az osztó között. Törtek szorzásánál/osztásánál nemcsak a törteket önmagában, de a törtek között is lehet egyszerűsíteni: szorzásnál „keresztben”, osztásnál „vízszintesen”.
1. Közönséges törteket úgy adunk össze illetve vonunk ki egymásból, hogy előtte közös nevezőre hozzuk őket, majd az adott műveletet a számlálókon végezzük el, az eredmény nevezője a közös nevező lesz. Akkor sem kell megijedni, ha a műveletben egész szám is szerepel. Ekkor az egész számot átírjuk 1 nevezőjű törtté, és máris csak törtjeink vannak (pl. 2 = 2/1).
2. Közönséges törtek szorzása/osztása: „számlálót a számlálóval, nevezőt a nevezővel”. Nem tévedés, osztás esetén is igaz ez a szabály! De mivel nem mindig oszthatók maradék nélkül a számlálók és a nevezők is egymással, ezért osztásra másik szabály is van: „reciprokkal szorzunk”. Ez utóbbi szabály alkalmazásánál ne tévedjünk, az osztónak kell a reciprokát venni!
3. Közönséges tört hatványozása: a számlálót és a nevezőt is hatványozni kell.
Bár meg lehet lenni nélküle, gyorsítja a számolást, ha ismerjük a „törtek szorzása/osztása egész számmal” műveletekre vonatkozó szabályokat (ha nem, akkor az egész számból 1 nevezőjű törtet csinálva alkalmazhatjuk az előbbi szabályokat):
4. Törtet úgy szorzok egész számmal, hogy ha lehet, akkor osztom a nevezőt, ha nem lehet, szorzom a számlálót.
5. Törtet úgy osztok egész számmal, hogy ha lehet, akkor osztom a számlálót, ha nem lehet, szorzom a nevezőt.
Mindkét esetben az osztás lehetőségét nézzük meg először, így biztosan nem kell majd egyszerűsíteni a művelet elvégzése után. És jegyezzük meg, hogy bár ezeket a szabályokat egész számokra tanuljuk, tetszőleges számokra (így például akár tizedes törtekre is) igazak.
6. Vegyes törtekkel (amikor egész rész és tört rész is van) való számolás előtt legtöbbször közönséges törtté kell alakítani. Ez úgy történik, hogy az egész részt megszorozzuk a tört nevezőjével, és a szorzatot hozzáadjuk a számlálóhoz, a nevező pedig marad változatlan. Pl.: 2 3/4 = (2*4+3)/4 = 11/4. Ez alól célszerű kivételt tenni vegyes törtek összeadása/kivonása esetén azért, hogy kisebb számokkal számoljunk. Ehhez azt kell észrevenni, hogy a vegyes törtben van egy ki nem írt műveleti jel az egész rész és a tört rész között, mégpedig az összeadás jel! Azaz pl. 2 3/4 = 2 + 3/4. Ezt kihasználva vegyes törtek összeadása és kivonása esetén érdemes külön számolni az egészekkel és külön a törtekkel. Pl. 2 3/4 + 3 1/2 = (2+3) + (3/4 + 1/2). Kivonásnál vigyázni kell, hogy a tört rész is negatív előjelet kap! 2 3/4 - 3 1/2 = 2 + 3/4 – 3 – 1/2 = (2-3) + (3/4 - 1/2)
Pár hasznos tudnivaló, amire a korábbi évek felvételi első feladataiban rákérdeztek:
- Törtrész kiszámítása szorzással történik. Tehát pl. 2-nek a 2/3 része: 2*2/3
- Ha egy műveletben vegyesen szerepel tizedestört és közönséges tört is, akkor általában egyneműsíteni kell: vagy a tizedestörtet írjuk át közönséges törtté, vagy fordítva … ez ízlés dolga, mindenki számoljon abban a formában, ami jobban bejön neki. A végeredményt általában bármilyen formában megadhatjuk, ha mégsem, akkor arra a feladatban felhívják a figyelmünket.
- Közönséges törtet úgy írunk át tizedestörtté, hogy a számlálót elosztjuk a nevezővel. Tizedes törtet úgy írunk át közönséges törtté, hogy a számláló a tizedesvessző nélküli egész szám lesz, a nevező pedig egy olyan 10 hatvány, amelynek a kitevője az eredeti számban szereplő tizedesjegyek száma (pl. 2,52=252/100).
- 10 hatvánnyal úgy szorzunk, hogy a tizedesvesszőt annyival visszük jobbra, amennyi a 10 kitevője. Ha menet közben a szám végére érünk – egész számhoz jutunk – a még szükséges helyiértékekre 0-kat írunk. Osztás ugyanez, csak ekkor balra mozgunk.
- Ha egy számot kerekíteni kell, akkor a megadott helyiérték jobb oldali szomszédja dönti el, hogy mi történik. Ha tehát pl. százasokra kell kerekíteni, akkor a tízesek helyiértéken, ha századokra, akkor az ezredek helyiértéken álló számjegy dönt.
- Két egész szám legnagyobb közös osztója az a legnagyobb egész szám, amely mindkettőnek osztója. Ha ez 1, akkor a két szám egymással relatív prím. A legnagyobb közös osztó nem lehet nagyobb a kisebb számnál.
- Két egész szám legkisebb közös többszöröse az a legkisebb egész szám, amelynek mindkét szám osztója. A legkisebb közös többszörös nem lehet kisebb a nagyobb számnál.
- Ha két szám relatív prím (azaz nincs egynél nagyobb közös osztójuk), akkor a legkisebb közös többszörösük a két szám szorzata. Hasonlóan, ha két szám szorzatát elosztjuk a legnagyobb közös osztójukkal, akkor megkapjuk a legkisebb közös többszörösüket.
- Prímszámok azok a természetes számok, amelyeknek pontosan 2 pozitív osztójuk van (az 1 és önmaga). Létezik legkisebb prímszám, ez a 2, amely egyben az egyetlen páros prímszám. Ha egy természetes számnak 2-nél több pozitív osztója van, akkor összetett számnak nevezzük. Ezekből következik, hogy az 1 nem prímszám és nem összetett szám.
- Műveletvégzési sorrend: zárójel > hatvány > szorzás, osztás > összeadás, kivonás. Egyenrangú műveletek esetén az összeadás, kivonás tetszőleges sorrendben végezhető, szorzás-osztás esetén balról jobbra haladunk.
- A természetes számok a nemnegatív egész számok, azaz a 0; 1; 2, 3; … stb. Végtelenül sokan vannak, azaz nincs legnagyobb, de van legkisebb, ami a 0. Figyeljünk a megfogalmazásra! Nem azt mondtuk, hogy a pozitív egész számok, mert akkor a 0 kimaradna! Úgy is szokták mondani, hogy a természetes számok a pozitív egész számok és a 0.
2. feladat
A második feladatban mértékegységek átváltása történik, összeadás/kivonás műveletekkel kombinálva. Ezek tulajdonképpen rendkívül egyszerű egyenletek, amikben általában két azonos és egy másmilyen mértékegység szerepel, de természetesen valamennyien ugyanabból a fajtából. Sokaknak okoznak problémát ezek a feladatok, pedig valójában nagyon egyszerűek. Az tény, hogy ugyanúgy kell tudni az alapegységek közötti váltószámokat (hosszúság, tömeg, térfogat, idő), mint a szorzótáblát … nem lehet gondolkodni rajtuk. Viszont jó hír, hogy a hosszmértékekből származtatott terület- és térfogat mértékegységeket nem kell külön megtanulni, azok egyszerűen levezethetők az alapmértékek váltószámaiból. Nézzünk egy példát. 1m2 hány dm2? Tudjuk az alapmértékek közötti váltószámot: 1 m = 10 dm. Mivel a mértékegységeket 2. hatványra emeltük, a váltószámot is 2. hatványra kell emelni, azaz 1 m2 = 102 dm2. Hasonlóan, 1 m3 = 103 dm3. És ennyi. Ha tudjuk az alapegységek váltószámait, mindent tudunk. És itt is elég a közvetlen szomszédok váltószámait ismerni, hiszen „távolabbi” mértékek közötti váltószám számítható a köztes váltószámok összeszorzásával. Pl. 1 m = 10 dm; 1 dm = 10 cm; 1 cm = 10 mm, ezért 1 m = 10*10*10 mm.
Említést kell tennünk a térfogat mértékegységekről, mert ezekből két származtatási rendszer is van. Az egyik az űrmértékek (hl, l, dl, cl, ml), a másik pedig a hosszmértékekből származtatottak (m3, dm3, cm3, mm3). Mivel mindkét rendszerben megadhatjuk ugyanazt a térfogatmennyiséget, ezért szükség van valamiféle összehasonlítási lehetőségre, egy átjáróra a két rendszer között. Ez az átjáró pedig a következő: 1 dm3 = 1 l. (Ez azt is jelenti, hogy az egyenletben a dm3 helyett simán írhatunk l-t vagy fordítva, ha a feladat éppen azt kívánja.) Ezt nagyon kell tudni, szinte mindig rákérdeznek a felvételin! Ha tehát egy feladatban pl. m3-ről kell átváltani dl-re, akkor előbb a m3-t átváltjuk dm3-re, a dm3-t literre (ami tulajdonképpen abból áll, hogy a dm3-t átírjuk l-re), végül a litert átváltjuk dl-re.
Végül 2+1 tipp a feladatok megoldásához.
- Az egyenletekben általában két ugyanolyan mértékegység és egy ezektől különböző szerepel. Ezt a különbözőt váltsuk át a meglévőkre, így oldjuk meg az egyenletet, és végül, ha szükséges (ha éppen a különbözőt kellett megadni), váltsunk vissza. (Ha netán három különböző mértékegység szerepelne, akkor kettőt váltsunk át a harmadikra.)
- Az utolsó részfeladat kettős egyenlőség szokott lenni. A megoldás során mindig csak az egyiket vegyük figyelembe egyszerre, és utána foglalkozzunk a másikkal. Ha netán az egyik egyenlőséget nem sikerülne megoldani, attól a másikat még sikerülhet, mindenképpen próbáljuk meg!
- Legyen pl. a feladat a következő: 7 m2 – 5000 cm2 = ………………… cm2 = ………………… dm2. Tegyük fel az elképzelhetetlent, nem tudjuk az első egyenletet megoldani, azaz nem tudjuk, mit írjunk az első pontozott részre. Ekkor már biztosan pontot veszítünk, de mentsük ami menthető … írjunk be valamilyen számot, és ezzel oldjuk meg a második egyenletet, azaz váltsuk át helyesen ezt a számot dm2-re! Ha ezt helyesen végezzük el, 1 pontot fogunk rá kapni.
3. feladat
Ebben a feladattípusban megadott feltételeknek eleget tevő valamiket kell összeszámolni. Ezeket a valamiket általában betű- vagy számkombinációval kell megadni. A feladat könnyebb megértése érdekében példaként megadnak egyet a lehetőségek közül, és az összes többit (ritkábban meghatározott darabszámot) a felvételizőnek kell megkeresni.
Ezt a feladatot szokták szeretni a diákok (gondolom azért, mert itt nem kell számolni ????), de tapasztalatom szerint véletlenszerűen keresik a megoldásokat, ezért sokszor nem is találják meg mindegyiket, vagy ugyanazt a megoldást kétszer is beírják. Másik probléma, hogy a feltételeket nagyvonalúan kezelik, ezért azoknak nem megfelelő „megoldást” is jónak gondolnak. Pedig ez az egyetlen olyan feladat, ahol hibás megoldásért pontlevonás jár! Ezért nagyon fontos, hogy mielőtt jónak minősítünk egy lehetőséget, vessük össze a feltételekkel, hogy valamennyit kielégíti-e! Ügyelni kell arra is, hogy ha az elkülönített részben próbálkozunk, akkor a jónak vélt megoldásokat mindenképpen írjuk át a vastag bekeretezett részbe, mert csak az oda írt megoldásokat értékelik!
Ennél a feladattípusnál nagyon fontos, hogy találjunk valamilyen rendszert, amely segítségével megtalálhatjuk az összes lehetőséget, így biztosak lehetünk benne, hogy nem hagytunk ki semmit. Ez a rendszer bármi lehet, a lényeg, hogy ez alapján vizsgálva a lehetőségeket mindegyik sorra kerüljön. Nézzünk egy példát, mire is gondolok.
Az 1, 2, 3, 4, 5 számjegyek összes olyan sorrendjét keressük, amelyekre egyszerre teljesül,
hogy
– az első számjegy páros,
– az egymás mellett lévő számjegyek különbsége nem lehet 1.
Mivel összesen két páros számjegyünk van, a rendszer most lehet pl. az, hogy megnézzük először a 2-vel, majd a 4-gyel kezdődő lehetőségeket. Ha a sorrend 2-vel kezdődik, akkor a második helyen nem állhat 1 és 3, csak 4 vagy 5. A 2-vel kezdődő sorrendek tehát csak 2; 4; ... vagy 2; 5; … alakú lehet. Az első esetben még az 1; 3; 5, a második esetben az 1; 3; 4 számjegyeket kell még jó sorrendbe rakni. Mivel a 4 után nem következhet 3 és 5, így csak 2; 4; 1; …-gyel folytatódhat a sor, és ezek után a 3; 5 számjegyek tetszőleges sorrendben elhelyezhetők, így az első esetben két megoldást kapunk: 2; 4; 1; 3; 5 illetve 2; 4; 1; 5; 3. A második esetben 5 után csak1 vagy 3 következhet. Ha 2; 5; 1; … lenne a sorrend, akkor a maradék 3 és 4 számjegyek egymás mellé kerülnének, így nem teljesülne a feladat 2. feltétele, azaz ebben az esetben nem kapunk megoldást. Ha 2; 5; 3; … a sorrend, akkor a maradék 1 és 4 számjegyeket csak egyféleképpen rakhatjuk sorba, így kapjuk a következő megoldást: 2; 5; 3; 1; 4. Minden lehetséges 2-vel kezdődő esetet megvizsgáltunk, áttérhetünk a 4-gyel kezdődőkre.
Ha a sorrend 4-gyel kezdődik, akkor a második helyen nem állhat 3 és 5, csak 1 vagy 2. A 4-gyel kezdődő sorrendek tehát csak 4; 1; ... vagy 4; 2; … alakú lehet. Az első esetben még az 2; 3; 5, a második esetben az 1; 3; 5 számjegyeket kell még jó sorrendbe rakni. Az első esetben 3. számjegyként a 3 vagy az 5 jöhet szóba. Ha 5 lenne, akkor a maradék 2; 3 számjegyek egymás mellé kerülnének, tehát így nem kapunk megoldást. Ha 3, akkor a maradék 5 és 2 számjegyeket csak ebben a sorrendben írva kapunk megoldást: 4; 1; 3; 5; 2. A második esetben 3. számjegyként csak az 5 jöhet szóba, és a maradék 1 és 3 számjegyek tetszőleges sorrendben elhelyezhetők, így újabb két megoldást kapunk: 4; 2; 5; 1; 3 illetve 4; 2; 5; 3; 1.
Mivel a kitalált rendszerünk mind a két lehetséges kezdő számjegyet, majd utána minden lehetséges folytatást megvizsgált, biztosak lehetünk benne, hogy minden megfelelő sorrendet megtaláltunk.
4. feladat
A 4. feladatban valamilyen diagramról (oszlop-, vonal-, kör- stb.) kell adatokat leolvasni. A tengelyes diagramok esetében először is állapítsuk meg, hogy melyiken milyen adatot tudunk leolvasni, illetve a rajtuk feltüntetett beosztások milyen értéknövekedést jelölnek. Amennyiben a diagram két vagy több grafikont tartalmaz, figyeljünk oda, hogy az adott kérdés melyikre vonatkozik! Kördiagram esetén általában azt kell meghatározni, hogy bizonyos körcikkek a körterület hányadrészét fedik le. Ehhez a kört valamilyen módon (ez feladatonként más és más) fel kell bontani egybevágó körcikkekre, és ezek segítségével már meghatározhatók (leszámolhatók) a tényleges körcikkek. Szinte mindig szükség van a körcikkekhez tartozó középponti szögek meghatározására is. Ehhez azt használjuk fel, hogy az egész körhöz 360 fokos középponti szög tartozik, és ez oszlik szét a körcikkek területeinek/ívhosszainak arányában. Kördiagramok esetében gyakori, hogy a feladat adatait vegyesen adják meg tört illetve % formákban. Ekkor egységesítsünk: törtet úgy írunk át %-ba, hogy megszorozzuk 100-zal és kiírjuk a % jelet; %-ot úgy írunk át törtbe, hogy osztunk 100-zal és elhagyjuk a % jelet. Oszlopdiagramok esetén erősen javasolom, hogy "0." lépésként minden oszlopra írjuk rá annak értékét, így a kérdések megválaszolásakor már csak le kell olvasni, nem kell minden alkalommal a figyelmünket elterelni.
5. feladat
Ebben a feladattípusban valamilyen síkidomot (sokszöget) mutatnak meg nekünk bizonyos feltételek teljesülése mellett, és pár szög nagyságát kell meghatároznunk.
Tapasztalatom szerint ettől a feladattípustól félnek leginkább a diákok, sokan hozzá sem fognak. Pedig talán éppen erre lehetne a legjobban felkészülni, hiszen pár alapismeret birtokában szinte „gondolkodás nélkül” automatikusan meg lehet válaszolni a kérdéseket. (Volt egy tanítványom, aki a felkészülés során ezeket a feladatokat mindig a végére hagyta, annyira nem szerette a geometriát. Végül a felvételin egyedül erre a feladatra kapott maximális pontszámot.)
Nézzük át, milyen alapismeretekre lehet szükségünk ennek a feladattípusnak a megoldásához.
- egy háromszög belső szögeinek összege 180 fok (ebből következik, hogy egy derékszögű háromszög két hegyesszögének összege 90 fok)
- egy négyszög belső szögeinek összege 360 fok
- ismerjük fel a mellék-, csúcs- és váltószögeket, és tudjuk, hogy a mellékszögek összege 180 fok, a csúcs- és váltószögek pedig egyenlők (nem kell feltétlenül tudni a nevüket, de felismerni őket mindenképpen)
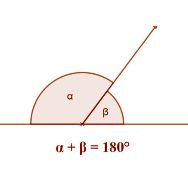Mellékszögek. Ha tehát a két szög egyikét ismerjük, a másikat megkapjuk, ha az ismert szöget kivonjuk 180 fokból.
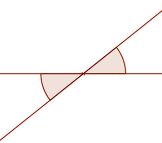
Csúcsszögek. A satírozott szögek egyenlők.
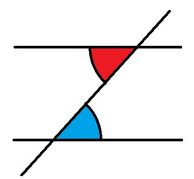
Váltószögek. Leggyakrabban „Z” betű formájában találkozunk velük. A piros és kék szögek egyenlők.
- egyenlő szárú háromszögben: az alapon fekvő szögek egyenlők (az egyenlő oldalak a szárak, a 3. oldal az alap); az alaphoz tartozó magasság felezi a szárszöget (a szárak által bezárt szöget) és az alapot is (ez fordítva is igaz: ha egy háromszögben egy oldalhoz tartozó magasság felezi az oldalt, akkor az a háromszög egyenlő szárú); egyenlő szárú háromszög esetén egyetlen szög ismeretében meghatározható a másik kettő: ha az alapon fekvő szög ismert, akkor a másik alapon fekvő szög ugyanekkora, a szárszöget pedig megkapjuk, ha 180 fokból kivonjuk az alapon fekvő szög kétszeresét; ha a szárszög ismert, akkor azt kivonva 180 fokból majd a különbséget megfelezve megkapjuk az alapon fekvő szöget
- egyenlő oldalú háromszög oldalai és szögei egyenlők, a szögei 60 fokosak; az ilyen háromszög másik neve: szabályos háromszög
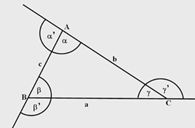- meg lehet lenni nélküle, de gyorsíthatja a munkát ha tudjuk, hogy egy háromszög külső szöge egyenlő a nem mellette fekvő két belső szög összegével; tehát α’=β+γ; β’= α+γ; γ’=β+α
Nagyon javaslom, hogy ezeknek a feladatoknak a megoldását úgy kezdjük, hogy az ábrába feltüntetünk minden olyan adatot, amely a szövegben szerepel, és még nincs jelölve az ábrán. Ha így teszünk, ezek után a szöveget már nem is kell néznünk, nem kell a szemünknek ide-oda ugrálnia. (Egyenlő oldalakra írjunk ugyanolyan kisbetűt, egyenlő szögeket jelöljünk ugyanolyan görög betűvel, szögfelezéskor jelöljük a félszögeket valamilyen görög betű/2-vel.) Hasonlóan, ha már meghatároztuk valamelyik keresett szög értékét, akkor azt ne csak a kijelölt helyére, hanem az ábrába is írjuk be!
Ezekben a feladatokban szinte mindig valamilyen speciális (egyenlő szárú, egyenlő oldalú esetleg derékszögű) háromszöget kell keresni úgy, hogy egyik szöge a kiszámítandó szög legyen, a másik kettőt pedig ismerjük vagy könnyen meghatározhatjuk az alapismeretek valamelyikével. Ezek után már könnyen kiszámíthatjuk a keresett szög értékét annak ismeretében, hogy egy háromszög belső szögeinek összege 180 fok.
6. feladat
kis türelmet
7. feladat
kis türelmet
8. feladat
kis türelmet
9. feladat
kis türelmet
10. feladat
kis türelmet
